Schwarzman Scholars worked together to create an academic journal, reflecting their ability to think critically about the Middle Kingdom and the implications of its rise. These collections of thoughts come together to form “Xinmin Pinglun,” our Journal dedicated to the publication of the informative and analytical essays of our scholars. As the application deadline for the class of 2019 is approaching and the arrival of the incoming class is on its way, we are sharing pieces from Ximin Pinglun to give insight into the critical thinking and scholarship taking place at Schwarzman College. Here, Larry Han, (Class of 2017) shares a story on his first Chinese New Year experience in China and the important life lesson he learned.
An unexpected 68-sided die
2017 marked the first year I spent the Chinese New Year (CNY) holiday in my motherland. As anyone who has celebrated CNY knows, one of the perks of being a student is receiving hongbao (red packets filled with money) from parents and relatives. However, sometimes the older generations will gamify the experience for children, in essence making them earn their New Year’s cash. My grandfather (Yeye), bless him, followed this mold. Over dinner on New Year’s Eve, Yeye reached into his pocket and took out a 68-sided die. “Why 68 sides?” I asked him. He replied that 68 was the largest number that could be expressed as the sum of two primes in exactly two ways: 68 = 31 + 37 = 7 + 61. Fun fact aside, Yeye introduced the game we would play as follows:
“Roll the 68-sided die twice. If the second roll gives a number larger than or equal to the first roll, then keep rolling. Continue rolling until the number rolled is smaller than the preceding roll. The game ends when this occurs. I will give you 100 yuan for each roll. For example, if you roll 23, 32, 66, 52, then you earn 400 yuan. How much money do you expect to win? I’ll give you 1,000 yuan if you get the correct answer. If you can generalize your expected winnings to an infinite-sided die, then I’ll add an extra 1,000 yuan.”
Two cases
I couldn’t believe that Yeye was going to make me work so hard for the hongbao I felt entitled to! After all, I had never even celebrated CNY in China. Shouldn’t I, of all people, be given an easy question? Well, Yeye did say that the solution was easy – I just couldn’t see it yet. I decided to approach the problem more generally, and then solve for the specific case of a 68-sided die afterwards. Here is what I wrote down:
Let’s suppose that I have an N-sided die. In solving for my expectedwinnings, the only thing I care about is the number that I just rolled.Thus, I can define f(n) to be the amount of money I expect to win if the last number rolled was n where 1 ≤ n ≤ N. But what should be my next step? Yeye, seeing my unease, offered another clue: tian rang zhi bie (天 壤之别). Unfortunately, I didn’t understand the Chinese idiom. Embarrassed, I asked for an explanation, to which Yeye replied, “Let your mind expand as far apart as heaven and earth and consider the extremes.”
Of course, the bounds! What if my first roll was a 1? Well, f(1) would be ideal because this is equivalent to a scenario in which the game really hasn’t started since any subsequent roll will allow the game to continue (I can’t roll a number smaller than 1). Thus, I want to eventually solve for f(1). Off to a good start, I next considered the 2 cases that could occur if I first roll n and next roll x:
(i) If I roll x ∈ {1, 2, …, n − 1}, i.e. x < n, then I win 100 yuan and the game ends. This case occurs with probability (n-1)/N.
(ii) If I roll x ∈ {n, n + 1, …, N}, i.e. x ≥ n, then I win 100 yuan and the game continues. I expect extra winnings of f(x) since the game continues. Since each roll x has probability 1/N of occurring, I can now write a recursion for my expected winnings f(n), defining an equation based on a previous iteration of itself.
[See 1 at end of article]. Now I can solve for my other boundary case, the scenario in which my first roll is n = N, or 68 here. In this case, [see 2]. Solving for f(N), I have that [see 3]. Thus, [see 4 and 5].
Thinking recursively
With a recursion in my back pocket, I hit yet another roadblock. “What approach do I take next?” I ask Yeye. He replies with another Chinese idiom, zhu ci jin si (逐次近似), or “consider successive approximate values.” Seeing my confusion, he rolls the die (32 appears) and asks me whether I ever considered what my expected earnings would be had I rolled a 31 or a 33 instead. I nod
my head and take the hint by rewriting the expected winnings recursion for n and n + 1 and considering the difference between the two, i.e. [see 6] which simplifies to [see 7]. Rearranging and solving for f(n), I have that [see 8].
Since N is a constant (68 here), I know that I can now evaluate recursivelyand solve for f(1) (the case that is equivalent to the game not having started yet, i.e. the expected winnings from this game). I observe that [see 9]. I can now use recursion to my advantage by substituting for f(2) into thefirst equation, i.e. [see 10]. I continue by substituting for f(3) so that [see 11].See the pattern? I can continue substituting for increasing values of n up to 68, i.e. the recursion can be extended up to f(N), i.e. [see 12] Remembering that I solved for the terminal condition f(N) earlier [see 4], I can substitute for f(N) and get that [see 13].
Checking that my solution is logical, I note that f(1) is undefined for N = 1. This makes sense since this would be equivalent to rolling a 1-sided die, in which case the same number is rolled each time and the game never ends! (since I never roll a number smaller than the previous roll).
So how much money do I expect to win in the 68-sided case? That, after all, is what I’m after. Since N = 68, I take out my phone’s calculator and type in [see 14].
“Correct!” Yeye yells excitedly. “You’ve unlocked 1,000 yuan” And for an infinite-sided die? Well, I type into my calculator progressively larger values for N, e.g. [see 15] and realize that my expected earnings are approaching a value that looks familiar. I can’t quite make out the significance though. Yeye sees my perplexed look and carefully considers what he should say before asking me, “Forget about the winnings. What is the expected number of rolls in this game?” Easy, I thought. That’s just my winnings divided by 100, so 2.7184. Look familiar? The lightbulb had gone on as I realized that as N →∞, Expected Rolls → e, Expected Winnings → 100e RMB.
The foolish old man
Before delivering my long-awaited hongbao, Yeye tells me a story, yu gong yi shan (愚公移山). Sitting upright on his stool, Yeye paints a scene of the rural, loess hillsides of northern China before introducing the Foolish Old Man of the North. Nearly 90 years old, he is unhappy that two mountains are blocking rays of vital sunlight for his crops. The old man calls on his entire family to help him level the mountains. One day his friend, the rational and level- headed Wise Old Man of the South comes over and says, “Stubborn old friend, at your age it is impossible for you to remove so much earth. You will kill yourself trying.” The Foolish Old Man pauses to think before responding, “You see, once I’m dead, my children will carry on the task. When my children die, I still have my grandchildren, who themselves will have children. Yet, the mountains do not grow. So why is it impossible to level the mountains?” The Mountain God, touched by the Foolish Old Man’s persistence, sends two titans to earth to help the Foolish Old Man level the mountains.
Yeye is 88 years old, and I can’t help but think of the parallel between his own story and the parable he has just told. My Yeye’s life has been defined by struggles, having experienced the Japanese occupation of China, the bloodshed of the Civil War, World War II, and the Korean War, the death of two sons before my father, the chaos and starvation of the Cultural Revolution, and the extreme pollution accompanying the unprecedented economic development of the past three decades. Overcoming these challenges is a testament to the fact that an unrelenting will and dogged persistence can help surmount seemingly mountainous obstacles. Even in solving a silly puzzle over Chinese New Year, firmness in pursuit of truth can lead to elegant, often unexpected outcomes.
The equations
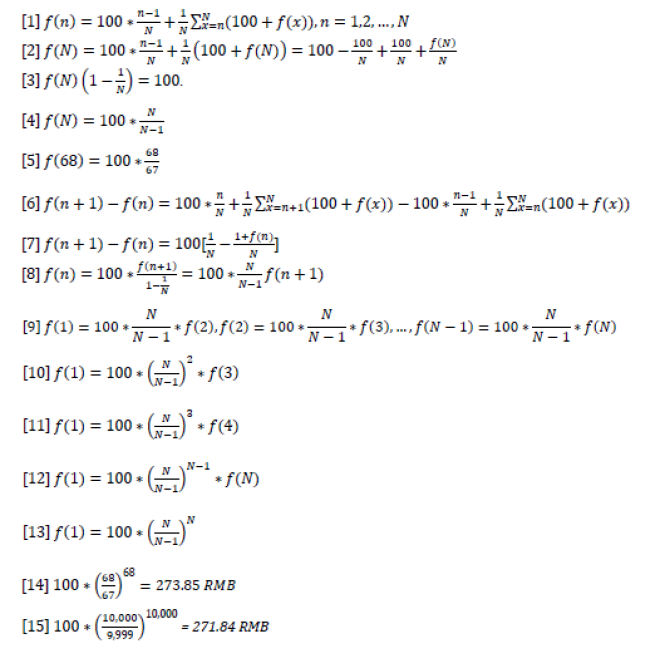
Larry Han (Class of 2017) is from the United States of America, and graduated from the University of North Carolina at Chapel Hill.